收敛函数是什么
在数学的广阔领域中,收敛函数是一个核心概念,尤其在分析学中扮演着至关重要的角色。为了深入理解这一概念,我们将从定义、性质、应用及实例等方面进行详细探讨。
一、收敛函数的定义
收敛函数,简而言之,是指当自变量趋近于某一特定值(通常是无穷大或某个有限值)时,其函数值也趋近于一个确定的极限值的函数。在数学上,这通常表示为:
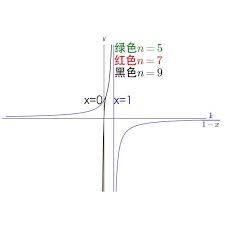
设函数⁄⁄(f(x)⁄⁄)在⁄⁄(x⁄⁄)趋近于⁄⁄(a⁄⁄)(或⁄⁄(x⁄⁄)趋近于无穷大)时,存在极限⁄⁄(l⁄⁄),即
⁄⁄[⁄⁄lim_{{x ⁄⁄to a}} f(x) = l ⁄⁄quad ⁄⁄text{(或} ⁄⁄lim_{{x ⁄⁄to ⁄⁄infty}} f(x) = l⁄⁄text{)}⁄⁄]
若上述极限存在,则称函数⁄⁄(f(x)⁄⁄)在⁄⁄(x⁄⁄)趋近于⁄⁄(a⁄⁄)(或无穷大)时是收敛的。
二、收敛函数的性质
收敛函数具有一系列重要的性质,这些性质在分析学、微积分及实数理论等多个数学分支中都有着广泛的应用。以下列举几个关键性质:
1. 唯一性:若函数在某点或无穷远处的极限存在,则该极限值唯一。
2. 局部有界性:若函数在某点处的极限存在,则函数在该点附近是有界的。
3. 保号性:若函数在某点处的极限为正(或负),则在该点附近,函数值将保持同号。
4. 夹逼定理:若存在两个收敛于同一极限的函数,且被研究的函数位于这两个函数之间,则被研究的函数也收敛于该极限。
三、收敛函数的应用
收敛函数的概念在数学的多个领域中都有着广泛的应用。在微积分中,它是求解极限问题的基础;在级数理论中,它决定了级数的和是否存在;在实数理论中,它用于定义连续性和可导性等概念。此外,在物理学、工程学及经济学等领域,收敛函数也是解决实际问题的重要工具。例如,在物理学中,收敛函数用于描述物理量的渐近行为;在工程学中,它用于分析系统的稳定性;在经济学中,它用于预测经济变量的长期趋势。
四、收敛函数的实例
为了更好地理解收敛函数的概念,以下列举几个典型的实例:
1. 常数函数:如⁄⁄(f(x) = c⁄⁄)(⁄⁄(c⁄⁄)为常数),对于所有⁄⁄(x⁄⁄),其极限均为⁄⁄(c⁄⁄),因此是收敛的。
2. 多项式函数:如⁄⁄(f(x) = x^2 + 2x + 1⁄⁄),在⁄⁄(x⁄⁄)趋近于无穷大时,其极限不存在,但在⁄⁄(x⁄⁄)趋近于有限值⁄⁄(a⁄⁄)时,其极限为⁄⁄(a^2 + 2a + 1⁄⁄),因此在该点是收敛的。
3. 指数函数:如⁄⁄(f(x) = e^{-x}⁄⁄),在⁄⁄(x⁄⁄)趋近于无穷大时,其极限为0,因此是收敛的。
4. 有理函数:如⁄⁄(f(x) = ⁄⁄frac{1}{x}⁄⁄),在⁄⁄(x⁄⁄)趋近于无穷大时,其极限为0;在⁄⁄(x⁄⁄)趋近于0时,其极限不存在(但可以说在⁄⁄(x=0⁄⁄)的右侧和左侧分别收敛于正无穷和负无穷)。
综上所述,收敛函数是数学中一个基础而重要的概念,它不仅在数学内部有着广泛的应用,也是连接数学与其他学科的重要桥梁。通过深入理解收敛函数的定义、性质及应用,我们可以更好地把握数学的本质,为解决实际问题提供有力的数学工具。
- 2025-06-30
- 2025-06-30
- 2025-06-29
- 2025-06-28
- 2025-06-28
- 2025-06-28
- 2025-06-27
- 2025-06-27
- 2025-06-26
- 2025-06-26
- 2025-06-26
- 2025-06-25
- 2025-06-25
- 2025-06-25
- 2025-06-24





